分析模拟音叉表晶有限元法得出怎样的结果?

来源：金洛鑫浏览：- 发布日期：2019-04-29 09:46:32【大中小】

分享到：

从上个世纪开始，32.768K频率小体积的圆柱音叉表晶，就被大量应用于各种电子产品，消费类产品身上，比较热门的是2*6和3*8这两种封装的，还有一种更小的5.0*1.5mm圆柱晶振。虽然品质和稳定性没有后来用的贴片晶振好，但是胜在价格低廉，适合大范围使用，降低生产工厂的成本。直到现在，仍有许多电子，钟表和其他中低端产品的工厂，仍在使用音叉表晶，国产或进口品牌都有使用。

这是针对几种类型支撑结构在32.768kHz下工作的小型石英音叉的初步研究。可以通过Euler-Bernoulli方程（精确解）计算齿长和齿宽，但由于基础设计的灵活性，基础应通过FEM（近似解）进行分析。有限元法（FEM）软件ANSYS用于模拟音叉石英晶体以从谐波分析中提取电响应。通过仿真比较几种类型的支撑结构与带凹口的改进音叉。

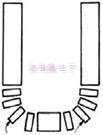
石英音叉的设计早期被视为U形模型，并且分析方法来自J.A.的传递矩阵法。Kusters和......等。在70年代。模型（图1）被分成几个部分，假设每个部分操作弯曲和长度-伸展模式，然后提取系统的特征频率。上述方法中石英音叉的底座不包括旋转惯性效应。90年代，HideakiItoh和......等。同时将石英音叉作为U形模型，类似于L形的右半部分由三个条组成，然后通过Sezawa的近似计算系统的特征频率。但在基础上，频率方程被认为是弯曲模式。基于Euler-Bernoulli方程的假设，该方程应适用于长杆而不是短杆（TuningForkBase）。在80年代，ShihS.Chuang介绍了包括转动惯量效应在内的弯曲模式的频率方程，包括转动惯量效应在内的频率方程适用于小长度与齿宽和小频率音叉晶振的比例。石英音叉采用了一种弯曲模式，由ShihS.Chuang开发。

图1.U形音叉模型

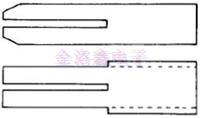
为了改善石英音叉的电气特性，YoshiroTomikawa提出了改进的基部宽度和臂角切断（图2）。这些想法确实用于实际产品中，以提高更好的电气特性，如更高的品质因数和更低的阻力等。2003年，FumitakaKitamura申请了一种新的基座形状-凹口，位于齿和安装区域之间（图3），以便在音叉晶体单元的小型化中获得良好的电气特性。

图2.改进的音叉，臂角被切掉，底座宽度为

图3.带凹口的改进音叉

众所周知，石英音叉单元已经在很多领域中使用，特别是在手表中使用了很长时间。由于手表的宽敞空间，音叉单元的尺寸不是最重要的问题。然而，音叉单元的尺寸问题更为重要，因为手机营销的增长和消费电子产品的多功能需求在过去十年中变得越来越强烈。石英音叉单元不仅需要满足狭小空间，还需要保持井电特性。如今，用于手机的音叉单元的流行封装尺寸为4.1x1.5mm和3.2*1.5晶振。最近，开发出最小的石英音叉单元2.0x1.2mm2。那些石英音叉单元比以前小很多。

对于小型石英音叉单元的设计，应减小齿长和底座长度以适应狭小空间。由于在32.768K晶振下运行的Euler-Bernoulli方程控制的齿的长度与齿的宽度之间存在关系，因此齿长的减小是有限的。因此，我们专注于基础形状的分析，以获得适当的基础形状和尺寸，以满足狭小空间和良好的电气特性的要求。

音叉的设计首先从Euler-Bernoulli方程中用无夹边界条件提取齿宽和齿长，然后用FEM软件（ANSYS，Inc。）模拟音叉晶振32.768K。封装尺寸为3.2x1.5mm，内部尺寸为2.45x0.8mm。几种类型的石英音叉单元支撑结构应与带有缺口的改进音叉进行比较（图3）。

从插件型到贴片型的转换不过十几年的时间，金洛鑫电子成立之初，也是从生产圆柱表晶开始做起的，到现在做的型号和类型也越来越多，但圆柱型的音叉晶体，仍有许多长期合作的客户在用。金洛鑫电子供应的1*5，2*6和3*8的圆柱晶体品牌主要有爱普生晶振，KDS晶振，精工晶振以及我们自己量产的JL品牌，如需详细资料或有意订购，请拨打咨询热线：0755-27837162，我们将为您提供完善的晶振服务！

下一篇：如何拖动振荡器中的晶振频率? 上一篇：为什么要重启精密石英晶振的频率?

您好，欢迎踏入金洛鑫电子有限公司

金洛鑫电子

分析模拟音叉表晶有限元法得出怎样的结果?

“推荐阅读”

相关常见问题

最新资讯文章